Angle Rules
Complementary & Supplementary Angles
| NAME | RULE | DIAGRAM |
| Complementary angles | Add to 90 degrees |  |
| Supplementary angles | Add to 180 degrees |  |
(Hint to remember these: C in the alphabet and 90 when counting both come before S and 180.)
Vertically Opposite Angles
| NAME | RULE | DIAGRAM |
| Vertically opposite angles | Equal |  |
Angles of Parallel Lines
| NAME | RULE | DIAGRAM |
| Corresponding angles | (F shape) |  |
| Co-interior angles | Add to 180 degrees (U shape) |  |
| Alternate angles | Equal (Z shape) |  |
Angles of Triangles
| NAME | RULE | DIAGRAM |
| Angle sum of triangle | Add to 180 degrees |  |
| Equilateral triangle | All angles equal 60 degrees |  |
| Isosceles triangle | Base angles are equal |  |
| Exterior angle of triangle | The exterior angle equals the sum of the two interior opposite angles. |  |
Question - Angle Sum of Triangle
To show that the angle sum of a triangle equals 180 degrees, draw a triangle, tear the angles and rearrange them into a straight line. Remember that the number of degrees in a straight line is 180 degrees.
Do a similar activity to show that the angles of a quadrilateral add to 360 degrees.
Angles of Quadrilaterals
| NAME | RULE | DIAGRAM |
| Angle sum of quadrilateral | Add to 360 degrees |  |
| Opposite angles of parallelogram | Equal |  |
Angles of Circles
| NAME | RULE | DIAGRAM |
| Radius meets tangent | The radius meets the tangent at right angles. | 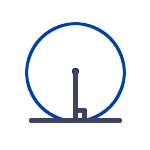 |
| Angle at centre | The angle subtended at the centre of the circle is twice the angle at the circumference. (arrow shape) |
 |
| Angle at circumference | Angles subtended by the same chord are equal. (butterfly shape) |
 |
| Opposite angles of cyclic quadrilateral | Equal |  |
| Exterior angle of cyclic quadrilateral | The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle. |  |

| 
| 
|