Conics

There are 4 graphs that are formed when a cone is sliced by a flat surface. These conic sections are:

• Parabola
• Circle
• Ellipse
• Hyperbola

---

Circle Equations

The Extreme Orbiter above consists of five rotating arms with three pairs of spinning seats on each arm. The engineer who designed this carnival ride used this equation of a circle which is based on Pythagoras' Rule.

( x – h )² + ( y – k )² = r²

where
(h,k) is the centre
r is the radius of the circle.

---

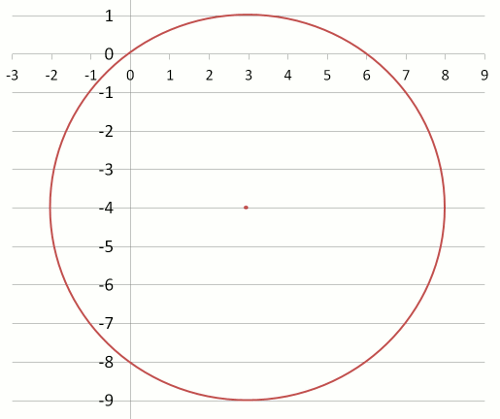
Example One

Find the coordinates of the centre and the length of the radius of a circle whose equation is:

( x – 3)² + ( y + 4 )² = 25.

Then draw this circle on grid paper.

Answer:
Centre = (h,k) = (3, –4)
Radius = 5

---

Ellipse Equations

( x – h )2	+	( y – k )2	= 1
a2		b2

where
(h,k) is the centre
a is half of the major axis
b is half of the minor axis of the ellipse.

---

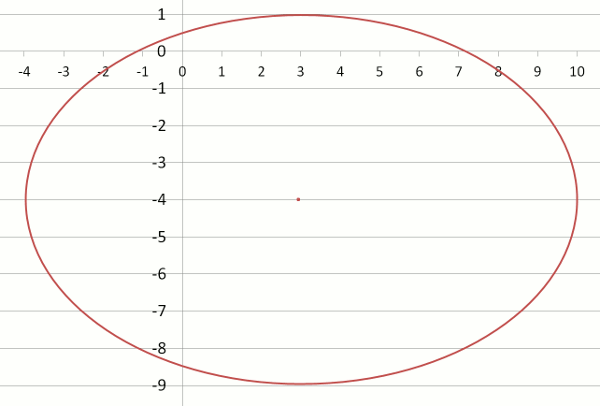
Example Two

Find the coordinates of the centre and the lengths of the axes whose equation is:

( x – 3 )2	+	( y + 4 )2	= 1
49		25

Answer:
h = 3
k = –4
a = 7
b = 5

Centre = (h,k) = (3, –4)
Length of major axis = 7 × 2 = 14
Length of minor axis = 5 × 2 = 10

---

Hyperbola Equations

The light given out by this lamp forms hyperbolas.

---

Example Three

Draw the graphs of the following hyperbolic equations. What do you notice?

(a)	y =	1
		x

(b)	y =	1
		x – 3

(c)	y =	5
		x – 3

(d)	y =	5	+ 4
		x – 3

Answers:

(a)

(b)

(c)

(d)